Degree of Static & Kinematic Indeterminacy of Structures

A structural system that can be analyzed by using the equation of static equilibrium only is called statically determinate structure i.e. reaction components and internal stresses can be calculated using static equilibrium equations only. Eg: Simply supported beam. If it cannot be analyzed by the equation of static equilibrium alone, then it is called a statically indeterminate structure. Eg: Fixed beam. A structural system is said to be kinematically indeterminate if the displacement components of its joints cannot be determined by the compatibility equation alone. Eg: Simply supported beam. If those unknown quantities can be found by using compatibility equations alone then the structure is called kinematically determinate structure. Eg: Fixed beam. But before calculating the degree of indeterminacy of a structure, it is good to know about its stability. If a structure is unstable, then it doesn't matter whether it is statically determinate or indeterminate. In all cases, such types of structures should be avoided in practice.

Stability of a Structure

The stability of a structure is of the following types:

External Stability
Internal Stability

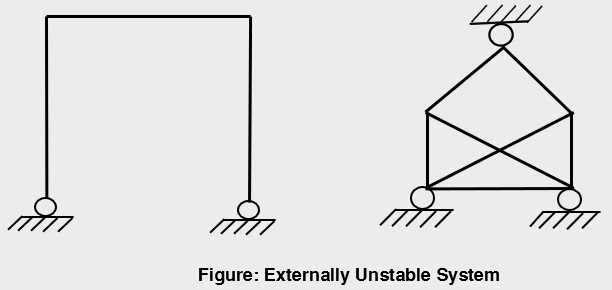
External Stability

For a structure to be externally stable, the reactive forces should be non-parallel & non-concurrent.

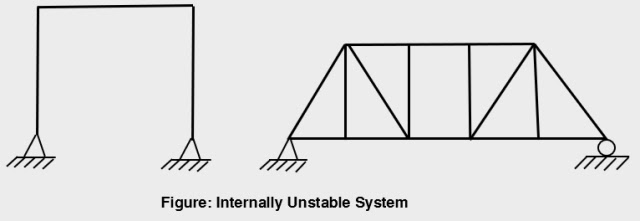
Internal Stability

An internally unstable system can change its shape without any deformation of its members.

Indeterminacy of a Structure

The degree of static indeterminacy or degree of redundancy shows the number of additional equations required to solve the system. External indeterminacy is related to the support system of the structure whereas internal indeterminacy is related to the internal stress in the members of the structure. The degree of kinematic indeterminacy shows the number of unknown joint deformations.

Degree of Static Indeterminacy of Pin Jointed Plane Frame ( Plane Truss )

The simplest form of a stable plane truss is a triangle having three members & three joints. Then, for each additional joint, two extra members are required. In this way, a stable & internally determinate truss system can be formed. Thus, considering all the joints except the first three joints (that form the basic triangle), 2(j-3) number of members will be required. And then adding the first three members that form the basic triangle, the total number of members in a truss can be formulated as below:

m = 2(j-3) + 3

or, m = 2j - 6 + 3

or, m = 2j - 3

where,

m = number of members

j = number of joints

Hence, if a plane truss is formed with 2j - 3 members (since, m = 2j -3) & if they are arranged in a suitable manner that the system cannot change its shape without deformation of its members, then a stable & internally determinate plane truss is formed.

Thus, the Degree of internal indeterminacy for a plane truss is m - (2j - 3).

The equations of static equilibrium available in order to find reaction forces in a plane truss is 3 (H = 0, V = 0, M= 0). If 'r' be the number of unknown reaction forces, then the degree of external indeterminacy related to the support system is r - 3.

Thus, the Degree of external indeterminacy for a plane truss is r - 3.

Finally, the total degree of static indeterminacy is the summation of the degree of internal indeterminacy & the degree of external indeterminacy.

An alternative approach for the determination of the degree of indeterminacy of a structure is to take a unified view without considering external and internal indeterminacies separately. In a plane truss, the total number of unknowns will be (m + r) as there will be a single unknown force (either tensile or compressive) in each member & the remaining unknowns will be reaction forces. Also, 2j independent equations will be available as two equations of static equilibrium (H = 0, V = 0) are applicable in each joint. Thus, the total degree of static indeterminacy for a pin-jointed plane frame is (m + r) - 2j.

Conclusion

Degree of external indeterminacy: r - 3

Degree of internal indeterminacy: m - (2j -3)

Degree of static indeterminacy: Degree of external Indeterminacy + Degree of internal indeterminacy

if m < 2j - 3, internally unstable

if m = 2j - 3, stable/unstable, statically determinate internally if stable internally

if m > 2j - 3, overstiff, statically indeterminate internally

Alternatively,

Degree of static indeterminacy: (m + r) - 2j

if (m + r) < 2j, unstable

if (m + r) = 2j, stable, statically determinate

if (m + r) > 2j, stable, statically indeterminate

Example

Degree of static indeterminacy of a truss

Degree of external indeterminacy = r - 3 = 6 - 3 = 3

Degree of internal indeterminacy = m - (2j - 3) = 3 - (2*4 - 3) = -2

Degree of static indeterminacy = External + Internal = 3 -2 = 1

Alternatively,

Degree of static indeterminacy = (m + r) - 2j = (3 + 6) - 2*4 = 1

Degree of Static Indeterminacy of Rigid Jointed Plane Frame (Plane Frame)

In a plane frame, the total number of unknowns will be (3m + r) as there will be three unknowns (axial force, shear force & bending moment) in each member & the remaining unknowns will be reaction forces. Also, (3j + c) independent equations will be available as three equations of static equilibrium (H = 0, V = 0, M = 0) is applicable in each joints plus 'c' equations of condition will also be available in some cases (eg: internal hinge, internal roller etc). Thus, the total degree of static indeterminacy for a rigid jointed plane frame is (3m + r) - (3j + c).

Here, m, r & j have their usual meaning & are easy to determine but the equation of condition 'c' needs to be understood well before moving on. The equation of condition provides extra equations in addition to the three equations of static equilibrium. Let's say, an internal hinge is provided at the center of the prop cantilever beam, then the moment about the internal hinge is zero from either side of the internal hinge. This means, two equations can be written by equating total moments to zero from the left side of the internal hinge & from the right side of the internal hinge. But these two equations are not independent because if the moment of all the forces left of the internal hinge is zero then the moment of forces on the right of the internal hinge is zero by default since the summation of the moment at an internal hinge is always zero. Thus, only one equation of condition (i.e. c = 1) will be available in such a case. If there are three members meeting at a single internal hinge (like in complex frames), then three equations can be written equating moments to zero. But there will be only two independent equations (i.e. c = 2) available since if two members at a hinge provide zero moments then the moment of the third member is automatically zero as the sum of moments at an internal hinge is zero. Now, while calculating indeterminacies, the value of 'c' can be determined by the simple formulation as below:

Equation of Condition(c) = Number of members connected to an internal hinge - 1

Conclusion

Degree of static indeterminacy: (3m + r) - (3j + c)

if (3m + r) < (3j + c), unstable

if (3m + r) = (3j + c), stable/unstable, statically determinate if stable

if (3m + r) > (3j + c), stable/unstable, statically indeterminate

Example

Degree of static indeterminacy of a frame

Degree of static indeterminacy = (3m + r) - (3j + c)

= (3*10 + 6) - (3*9 + 3) since, c = (3 - 1) + (2 - 1)

= 36 - 30

= 6

Degree of Kinematic Indeterminacy of Pin Jointed Plane Frame (Plane Truss)

Each joints of a plane truss has two independent displacement components as they can have translation along x & y direction. The degree of kinematic indeterminacy (or degree of freedom) for a plane truss can be written as: 2j - e

where, e is the number of compatibility (boundary) conditions known.

As all the members of a truss system are considered to be extensible (or axial deformation is considered for every truss), the boundary conditions( value of e) will be obtained only from support conditions & will be equal to the number of reaction forces (r). Hence, the degree of kinematic indeterminacy for a plane truss is equal to 2j - r.

Conclusion

Degree of kinematic indeterminacy for plane truss: 2j - r

Example

Degree of kinematic indeterminacy of a truss

Degree of kinematic indeterminacy = 2j - r = 2*8 - 3 = 13

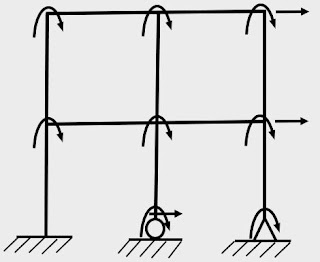
Degree of Kinematic Indeterminacy of Rigid Jointed Plane Frame (Plane Frame)

Each joint of a plane frame has three independent displacement components as they can have translation along x & y-direction as well as rotation about the z-axis. So, the degree of kinematic indeterminacy for a plane frame can be written as: 3j - e

If the members of the plane frame are considered to be extensible, then the external supports only will provide the boundary conditions & the number of compatibility equations(e) will be equal to the number of reaction forces (r). The degree of kinematic indeterminacy for a plane frame is then equal to 3j - r. But if the members of the plane are considered to be inextensible, then boundary conditions will also be obtained from inextensibility in addition to support conditions. The number of additional boundary conditions due to inextensibility in an unbraced plane frame is equal to the number of members in the frame system. And hence, the degree of kinematic indeterminacy for the unbraced plane frame is equal to 3j - (r + m). This is valid only for an unbraced plane frame system. In the case of a plane braced frame, it is convenient to count the degree of freedom for each joint by visual inspection rather than using a formula.

Conclusion

If plane frame is extensible, degree of kinematic indeterminacy: 3j - r

If plane frame is inextensible & unbraced, Degree of kinematic indeterminacy: 3j - (r + m)

If plane frame is inextensible & braced, count the degree of freedom by visual inspection.

Example 1 (Unbraced Extensible Frame)